ICFPC 2021 に参加しました
ICFPC 2021 にチーム「グレースたなか」として参加しました。 メンバーは cos, nojima, qwerty, seikichi の4人です。また、チームのリポジトリは https://github.com/seikichi/icfpc2021 にあります。
問題
今年の問題はポーズをうまく変形して穴をくぐるというものです。穴をくぐることができれば成功で、ポーズの良さに応じた点数を獲得できます。穴の各頂点にポーズの頂点が近いほどそのポーズは良いとされています。以下の gif を見るとイメージしやすいでしょう。

ポーズは好きなように変形できるわけではありません。辺の長さが大きく変わるような変形は禁止されています。どれぐらいなら辺の長さが変わってよいかは問題ごとに定められています。また、頂点の座標は整数でなければなりません。
問題の一覧は公式サイトにあります。
1日目
今年の ICFPC は金曜日の午後9時から始まりました。いつもどおり、自分と cos さんとでペアプロして入力を読むところから実装を開始します。ソルバーの実装には今年も Rust を使いました。Rust を使う機会が ICFPC しかないので、一年ぶりの Rust となります。
まずはヘボくてもいいので動くものを、ということで、ポーズ全体を平行移動・90度回転・鏡像反転するソルバーを作りました。これらは候補数が少ないので単純に全探索できます。
また、seikichi さんが整数計画ソルバーを使って厳密解を求める AI を作っていました。12番や16番のように頂点数の少ない問題に対しては一瞬で厳密解が出るようです。
ここらで深夜3時近くになってきたので寝ます。
9時ぐらいに起床しました。
1日目終了時点でライトニングラウンドがあるので、とりあえず悪い解でもいいから全部の問題に対して何かしらの解を用意しないといけません。そこで、適当に valid な解を見つけてくる DFS ソルバーを作りました。これは穴の中の点を一つ選んで、ポーズの頂点をそこに置くという操作を繰り返すだけのナイーブなソルバーです。
1番の問題をソルバーで解かせてみたら遅すぎて解が出ませんでした。そこで、重要そうな頂点から先に置くというヒューリスティックを入れたら解が出てくるようになりました。各頂点の重要度は (すでに確定している頂点だけを考慮したときの次数, すべての頂点を考慮したときの次数) で定めました。
このソルバーの出力する解は、ぐちゃぐちゃに折りたたまれた糸くずの塊みたいな形になっていて、どう見てもスコア的には酷いものでしたが、とりあえず解が出たのでヨシ!
seikichi, qwerty ペアは問題と解を一覧で見れるサイトを作っていました。公式サイトは問題ごとにページ遷移しないといけないので、すべての情報を1ページにまとめたサイトを作っておくと検討効率が大幅に上がります。CDK と Amplify が便利とのこと。
DFSソルバーがそれなりに動いているので、出てきた解を改善すべく山登り法ソルバーを追加。これは初期解を受け取って「頂点をランダムに動かしてスコアが改善するならそれを採用する」という手順を繰り返すソルバーです。
山登り法が動いたので次はアニーリング法を試しました。山登り法よりもアニーリング法の方がスコアが改善することがわかったので以降はアニーリングソルバーをメインで使っていくことに。
そのあとは適当にソルバーを高速化したり、アニーリングの途中で参照するスコアに頂点の分散を加味するように修正したりしていました。
ソルバー班と並列してインフラ班が解を提出するスクリプトを書いてくれていたので、それを使ってライトニング用の解を提出し、一日目は終了しました。
2日目
問題に「ボーナス」という仕様が追加されました。問題で指定された場所にポーズの頂点を配置すると特定の効果を持つボーナスを取得でき、他の問題でそれを使用できるというものです。とはいえ、今の自分たちのソルバーではボーナスを活用できそうにないので、当面はボーナスを無視して既存のソルバーの改善を続けることに。
そして2日目の朝。
アニーリング法ではなく、グラフのエッジをバネとみなして物理法則をシミュレートする方式で解を作ってみるとどうだろうかと思って物理ベースソルバーを作ってみました。しかし、壁に埋まったバネがすごい勢いで遠くにぶっ飛んでいく現象(ゲームでまれによく見るやつ)が多発してまともに動きませんでした。
一方、cos さんはポーズの頂点を(制約を満たさない位置に)移動させ、そのあと制約を満たすように周囲の頂点の座標を調整するようなルーチンを作っていました。このルーチンを使って初期ポーズを shrink して穴にはめ込むソルバーが作られ、(DFS ソルバーだと解が求まらないような) 頂点数が多い問題に対して解を出力することができるようになりました。
別の DFS も試してみたいということで、頂点ではなく辺を置いていく DFS ソルバーを作りました。与えられたグラフを橋で分解すると複数個の2-連結グラフになります。2-連結なグラフは耳分解ができるので、耳を順番に置いていく感じで DFS をします。これにより、それぞれの耳がどの頂点に戻ってくるかが事前にわかるので、絶対に戻ってこれないような座標に頂点を置かないように枝刈りすることができます。また、直前に置いた辺と同じ方向に優先して置くことで、潰れた解を避けやすくできます。
seikichi さんは整数計画ソルバーの改善をやっていました。何をやっていたのかは把握していません。すまぬ…。
あとはアニーリングソルバーのベンチマークをとって高速化をするなどしてました。cargo flamegraph で簡単にこんなグラフが出てくるので便利。
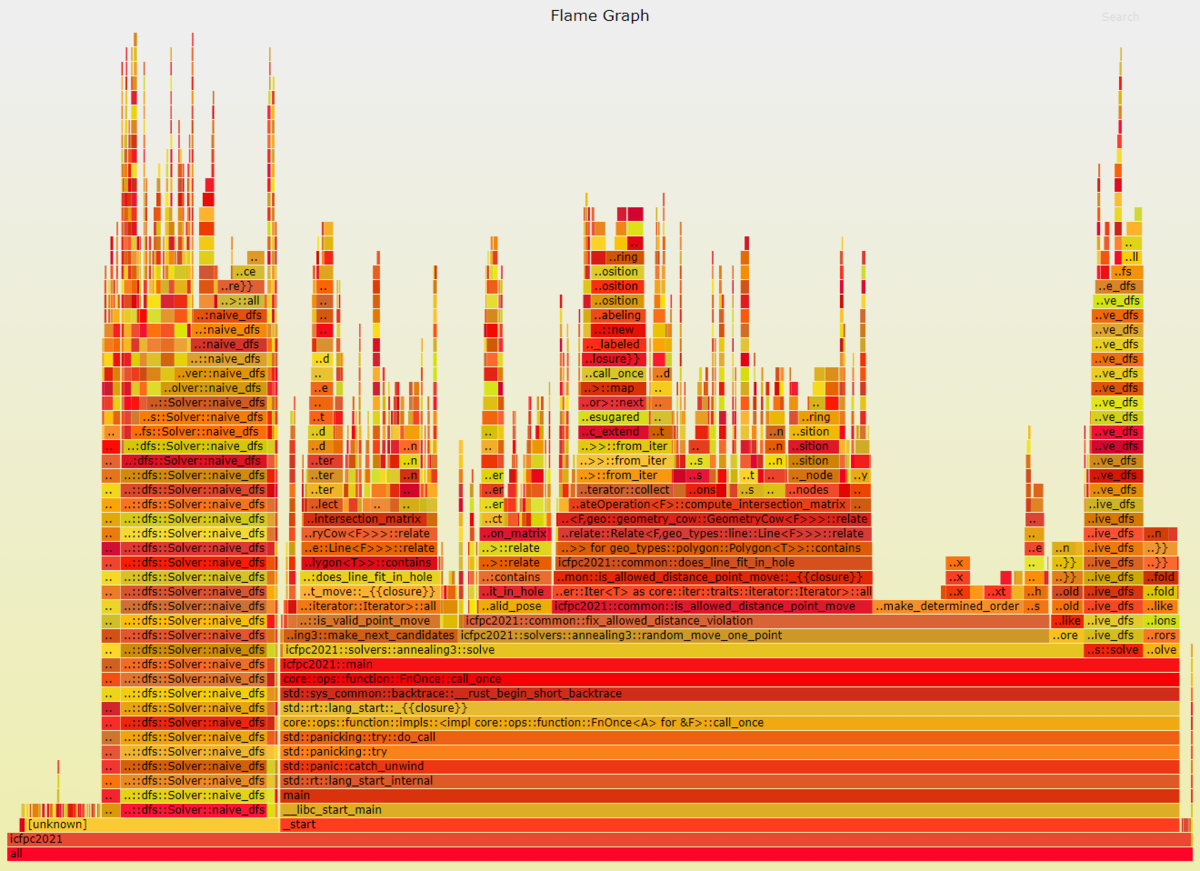
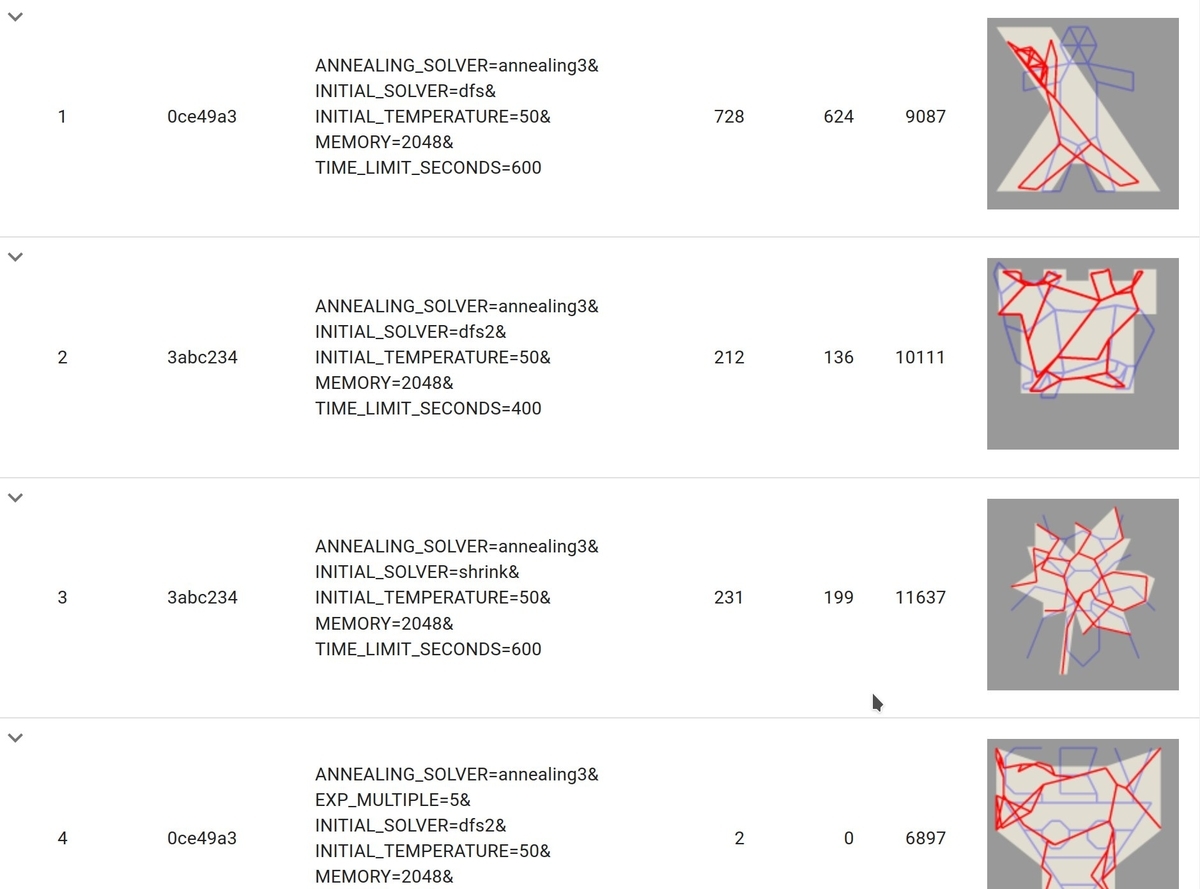
また、seikichi・qwerty ペアは AWS で Lambda でソルバーを並列実行して、結果を DynamoDB に保存する仕組みを作っていました。パラメータごとの結果を WebUI から確認できるのでソルバーの改善に役立つ優れものです。
3日目
DFS をビームサーチに変えてみたり chokudai サーチにしてみたりしましたが、単純な DFS より良くはなりませんでした。
seikichi さんが整数計画ソルバーを改善しているのを横目にこの日は寝ました。
そして3日目の朝。
cos さんがアニーリングソルバーに頂点を穴の外周に向かって引っ張るようなムーブを追加しました。このヒューリスティックがかなり効いて多くの問題のスコアが伸びました。
最終日ということもあり、ソルバーを走らせる時間も Lambda の実行時間の限界である15分近くに設定するようになりました。実行時間を伸ばすことでアニーリングソルバーの解が露骨に改善されました。AWS への課金が捗りますね。これが金の弾丸…!
AWS のコンソールを見ると並列で実行されている雰囲気がわかります (これはアニーリング10分で実行したときのやつです。たぶん)。
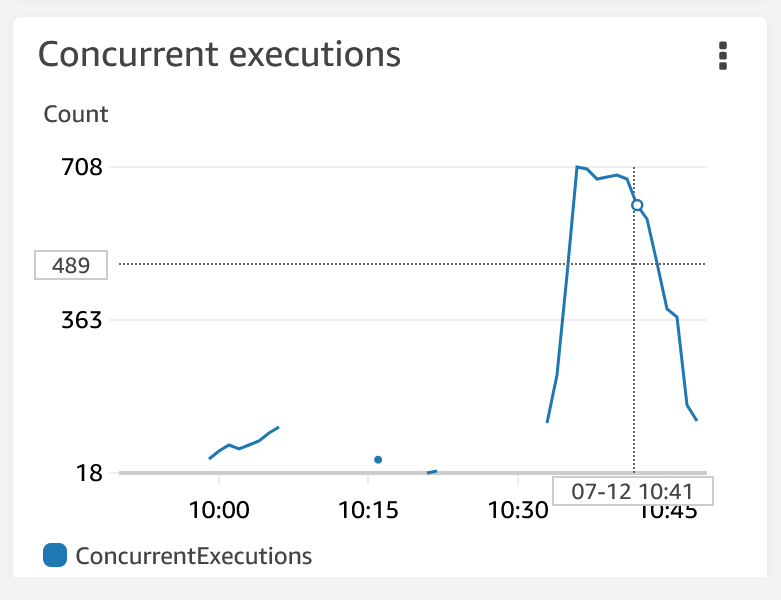
夕方からはアニーリングの最適な初期温度を調べていました。大幅にスコアが上がったりはしませんでしたが、無視できないぐらいにはスコアが改善されました。
最後に、すべての問題を最新のソルバーで解きなおしたり、スコアの上がり幅が大きそうな問題に対して乱数ガチャ(乱数シードを変えながらアニーリングを連打する)をしたりして、提出する解をつくりました。
順位は 20 位でした。お疲れ様でした。
完走した感想ですが
Clean Architecture では AP のデプロイをどう扱うべき?
インフラ的なコードを Clean Architecture を使って設計するとき、デプロイはどう扱ったらいいんだろうか?
エンティティの永続化
デプロイについて考える前に、より馴染みのある「エンティティの永続化」について考える。
例えば、User というエンティティを MySQL を使って永続化する場合、どのような設計にするだろうか?
よくあるパターンでは、
- ドメイン層に UserRepository というインターフェイスを作る。
- UserRepository を使って User の永続化に関するビジネスルールを記述する。
- アダプタ層で UserRepository を実装したクラス MySqlUserRepository を作る。
みたいな感じになる。
エンティティのデプロイだとどうなる?
デプロイでも永続化と同じような設計ができるのでは?と最近考えてる。
ApServer というエンティティを Kubernetes 上にデプロイする状況があるとする。 このとき、以下のような設計にすると見通しがよいのではないだろうか:
- ドメイン層に ApServerDeployer というインターフェイスを作る。
- ApServerDeployer を使って ApServer のデプロイに関するビジネスルールを記述する。
- アダプタ層で ApServerDeployer を実装したクラス KubernetesApServerDeployer を作る。
永続化の例との対応は以下のようになる。
| 永続化 | デプロイ | |
|---|---|---|
| エンティティ | User | ApServer |
| インターフェイス | UserRepository | ApServerDeployer |
| 外部サービス | MySQL | Kubernetes |
| プロトコル | SQL | Manifest |
まだアイデアレベルで、この設計を実際に試したわけじゃないので、機会を見つけて試してみたい。
ぷよぷよのプレイ動画を解析して棋譜を生成する
この記事は KMC アドベントカレンダー の 3 日目の記事です。 昨日は PrimeNumber さんの PEZY-SC/SC2を使った話 でした。
背景と問題
ぷよぷよの上達を阻む問題として「自分の手が良いのか悪いのかわからない」という問題があります。 ツモが毎回ランダムであるため、仮に悪い手を指したとしてもその後のツモに救われて何とかなる場合もありますし、仮に良い手を指したとしてもその後のツモが悪いと形が崩れてしまう場合もあります。 ある手が良いか悪いを知るためには、何度も試行を重ねて統計的に判断しなければなりません。 これは非常に時間がかかります。
幸いなことに、現在多くの上級者が YouTube にプレイ動画をアップロードしています。 プレイ動画を解析して上級者がある局面でどういう手を指したかどうかを知ることができれば、それを使って自分のプレイを評価できるのではないでしょうか?
しかし、プレイ動画はそのまま統計処理できる形式ではありません。 統計処理に適した形式、つまり棋譜(= 手順をテキストとして書いたもの)に変換する必要があります。
そこで今回、ぷよぷよのプレイ動画を解析して棋譜を生成するプログラムを作ったので、その紹介をしていきます。
解析に用いた動画
このプログラムを作るにあたり『ぷよぷよクロニクル 第2回おいうリーグ S級リーグ ようかん vs まはーら 50先』 をサンプルとして利用させていただきました。
使用した言語/ライブラリ
今回の動画解析は Python と OpenCV を使いました。Jupyter notebook で作業すると動画のフレームやメトリクスのグラフなどをインラインで描画できて便利でした。
↓ Jupyter notebook で動画の1フレーム目を描画している図:

フィールド上のぷよの認識
フィールドの枠の位置は時刻にかかわらず一定なので、今回は given ということにしました。 フィールドには横に6個、縦に12個のマスが等間隔で並んでいるため、枠の位置が決まればマスの位置も自動的に決まります。
次に、マスの状態(空、赤、黄、青、緑、紫、おじゃまの7状態)を判定します。 これは単純に状態ごとに予めパターン画像を用意しておいて、マスの画像とパターン画像との差分が最も小さかった状態を選ぶというアルゴリズムにしています。
下図の上の画像が (4, 4) に位置するマスの画像で、下の画像が赤のパターン画像との差分を取った画像です。 全体的に黒くなっていてそれっぽい感じがしますよね?
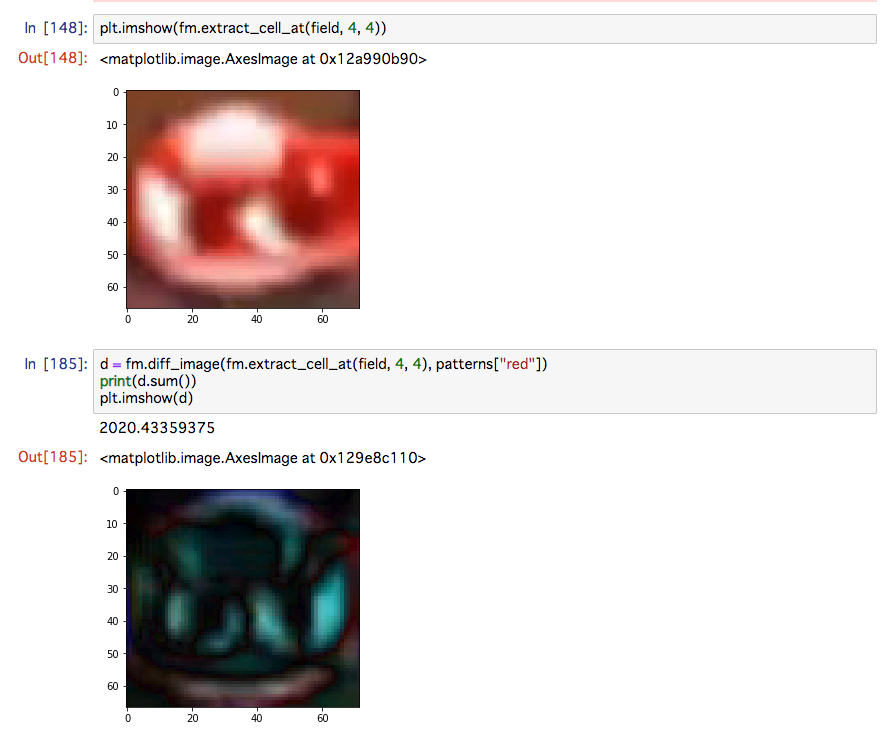
下図は実際のフィールドに対してフィールド認識した結果です。 左が与えられたフィールドの画像で、右が認識結果を使って作った画像です。 地面に設置しているぷよは正しく認識できていることがわかると思います。 一方で操作中のぷよは正しく認識できていません。 これは認識アルゴリズムがマス目単位で判定しているからです。

ぷよを置いた瞬間かどうかの判定
ぷよぷよの棋譜を生成したいという目的において、操作中のぷよが空中にある状態のフレームは不要です。 ぷよが接地し、場所が確定した瞬間のフレームこそが重要です。 ではどうやってぷよを置いた瞬間のフレームを識別すればよいでしょうか?
ぷよを置いたとき、次に起こりうることは次の3通りです。
- 次のぷよをツモる
- ぷよが消える
- おじゃまぷよが降る
そこで1から順に考えていきます。
1. 次のぷよをツモる瞬間の判定
あるフレームが次のぷよをツモる瞬間かどうかは、ネクスト欄およびダブルネクスト欄を見れば判定できます。
これらの欄はツモの瞬間にぷよがスライドし、次のぷよが表示されます。 これ以外のタイミングでは動きません。 したがって、これらの欄に変化があるかどうかを調べればぷよをツモったかどうかがわかります。
次のグラフはネクストぷよ表示欄について、1フレーム前とのピクセル差分の合計値を表しています。 x軸は時刻です。ツモったタイミングに合わせて値が跳ねているため、これの変化率を見ればツモの瞬間がわかります。
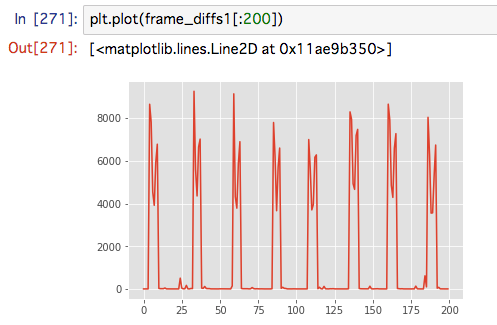
しかし、実際にやってみるとうまくいかない場合があります。 例えば下図のようなケースです。 連鎖光がネクスト欄に重なっており、ナイーブに判定するとツモったとみなされてしまいます。 今回はネクスト欄とダブルネクスト欄両方に連鎖光が重なることは少ないだろうということで、両方の欄で独立にツモ判定を行い、両方が true だった場合にツモったと判定することにしました。 しかし、絶妙な軌道で連鎖光が発射されると誤判定しそうなので、この判定の改善は将来の課題です。

また、ゲームのせいなのか動画のせいなのかわからないのですが、たまに連続する2フレームが全く同じ画像になっていることがあります。このときに1フレーム前とのピクセル差分を取るとゼロになってしまって誤判定します。今回は3フレーム前と比較することで回避しました。
2. ぷよが消える瞬間の判定
ぷよが消える瞬間はスコアを見れば簡単に判定できます。 ぷよが消えるときだけスコアは「数値×数値」という表示になります(普段は一つの数値です)。 なので×マークがあるかどうかをパターンマッチで判定することにしました。

x軸を時刻、y軸をピクセル差分としてグラフにプロットしてみました。 800フレーム目のあたりから13連鎖しているのが見てとれると思います。
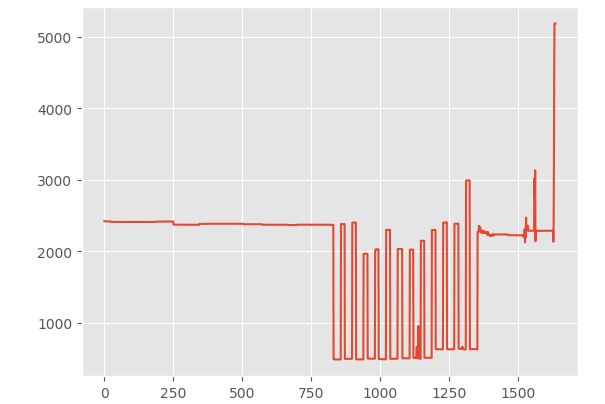
3. おじゃまぷよが降る
実はおじゃまぷよが降る場合は特に判別しなくても後処理で何とかできるので、処理していません。
情報を集約して棋譜を作る
これでぷよをツモる瞬間のフィールドの状況、ぷよが消える直前のフィールドの状況が時刻情報付きでわかったことになります。 後は連続する2つのイベントの間のフィールドの差分を取れば、どこにぷよを置いたのかがわかりますし、ぷよの消滅が連続して何回起こったのかを数えれば何連鎖したのかがわかります。
実際にある試合の様子を棋譜として出力してみたら以下のようになりました(1Pのみです)。 結構それっぽい棋譜ができました。
33: ▲1一黄 ▲2一青 59: ▲3一青 ▲3二紫 85: ▲2二紫 ▲2三青 108: ▲2四黄 ▲2五赤 135: ▲4一紫 ▲4二赤 160: ▲3三黄 ▲4三紫 186: ▲1二青 ▲1三黄 209: ▲3四赤 ▲3五青 237: ▲5一赤 ▲6一赤 261: ▲1四黄 ▲1五赤 288: ▲5二黄 ▲5三赤 316: ▲6二黄 ▲6三黄 339: ▲1六赤 ▲2六青 364: ▲6四赤 ▲6五赤 389: ▲5四黄 ▲5五赤 412: ▲5六紫 ▲6六紫 435: ▲6七紫 ▲6八赤 458: ▲4四青 ▲4五黄 479: ▲1七青 ▲1八青 499: ▲3六赤 ▲3七赤 520: ▲5七黄 ▲5八紫 538: ▲3八青 ▲3九青 560: ▲4六赤 ▲4七黄 581: ▲5九紫 ▲6九赤 601: ▲4八黄 ▲4九青 622: ▲5十青 ▲5十一紫 642: ▲6十青 ▲6十一赤 661: ▲6十二黄 681: ▲2七黄 ▲2八赤 700: ▲1九赤 ▲2九赤 718: ▲1十黄 ▲2十紫 759: ▲4十紫 ▲4十一紫 777: ▲4十二青 ▲5十二黄 804: ▲3十赤 ▲2十一黄 832: ▲3十一紫 ▲2十二青 発火 873: 2連鎖 914: 3連鎖 956: 4連鎖 996: 5連鎖 1038: 6連鎖 1082: 7連鎖 1122: 8連鎖 1162: 9連鎖 1203: 10連鎖 1244: 11連鎖 1286: 12連鎖 1327: 13連鎖 1397: ▲3一黄 ▲3二紫 1463: ▲3三黄 ▲3四赤 1529: ▲投了
661 フレーム目でぷよを1個しか置いていないことになっていますが、これは片方のぷよが画面外に置かれたからです。 また、おじゃまぷよの落下はこの棋譜には書かれていませんが、プログラムの中のデータとしては取得できています。
Future work
今のところ PoC レベルなので、実用にはまだまだ全然足りません。
まず、まだ 1P 側しか取れないので 2P 側も取る必要があります。 ゲームオーバー判定が背景に依存しているので背景が変わると動きません。 ぷよクロじゃなくてぷよスポにも対応したいです。 全消しの場合、パターンマッチが誤爆するかもしれません(試してない)。
暇を見つけてぼちぼちやっていきたいです。
まとめ
はじめての動画処理でしたが、意外と泥臭い力技で何とかなりました。 やってみるものですね。
明日は utgwkk さんの「レコード多相についてお話します」です。お楽しみに。
NLL のおかげで Rust で平衡二分木を実装できた
Rust で平衡二分木を書くのは何となく難しいイメージがありました。 unsafe を使わずに実装できるものなのか気になったので、試しに実装してみました。
結論から言うと、unsafe を使わなくても平衡二分木は実装できました。また、unsafe だけでなく、Rc や RefCell も使っていません。
ただし NLL がないとコンパイルが通りませんでした。NLL は神機能ですね。
Splay 木
今回実装した平衡二分木は Splay 木というものです。
Splay 木は、search や insert などの典型的な操作を償却 時間で実行できます。
また、Splay 木は最後にアクセスしたノードを木のルートに持ってくる性質があるため、アクセスに局所性がある場合によい性能が出るそうです。
平衡二分木といえば何と言っても赤黒木ですが、赤黒木は実装が大変すぎるので今回は却下しました。
アルゴリズム
Splay 木のアルゴリズムについては、Wikipedia に図付きで書いてあるので、こちらを参照下さい。
重要なのは Splay 操作 という操作で、これは特定のキーを持つノードをルートに持ち上げていく操作です。 この持ち上げていく過程でその周辺のノードが何となく平衡状態に近づくようになっています。
search や insert は Splay 操作を使って簡単に実装できます。
実装
BinaryNode
ノードは key と左右のノードを保持します。今回は簡単のため value は保持しませんでした。 ノードは左右のノードを 所有 していることに注意してください。
struct BinaryNode<K: Ord> { key: K, left: Option<Box<BinaryNode<K>>>, right: Option<Box<BinaryNode<K>>>, }
SplayTree
SplayTree は単に木のルートを保持しているだけです。
ノードが一つもない場合もあるので Option になっています。
pub struct SplayTree<K: Ord> { root: Option<Box<BinaryNode<K>>>, }
rotate
データ構造の準備ができたので、Splay 操作の実装に入ります。
まずは rotate_right です。
rotate_right は下図のように与えられた部分木のルートの左側のノードが新たなルートとなるように木を回転させる操作です。
もちろん、回転させるときにノードの順序関係は保つ必要があります。
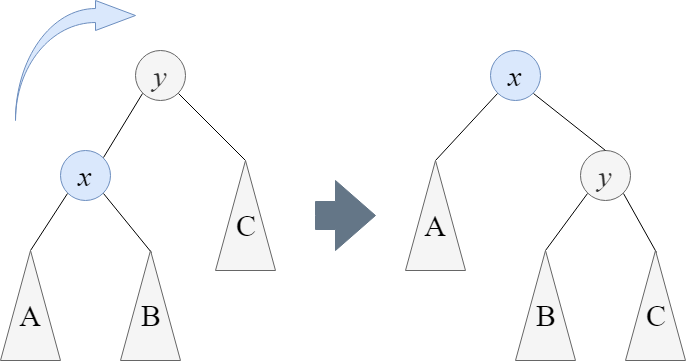
rotate_right の実装は以下のようになりました。
// root の左側のノードが新たな根となるように木を回転させ、新たな根を返す。 fn rotate_right<K: Ord>(mut root: Box<BinaryNode<K>>) -> Box<BinaryNode<K>> { let mut new_root = root.left.unwrap(); root.left = new_root.right; new_root.right = Some(root); new_root }
まず、引数としてルートとなるノードの 値 を取ります。参照ではありません。
つまり、rotate_right はルートノードの所有権を要求するということです。
そして、戻り値として新しいルートノードを所有権付きで返しています。
所有権が必要なのはノードの親子関係を弄るからです。 ノードの親子関係を変えるためには move する必要があり、move するにはそのノードを所有していないといけません。
また、関数の中身についてですが、実はこれ、NLL を有効にしないとコンパイルが通りません。 3行目でコンパイルエラーになります。
こういういかにも borrow check が難しそうなコードもちゃんとコンパイルしてくれる NLL は素晴らしいですね。
splay
rotate ができれば後は場合分けして splay 操作を実装するだけです。 key が左側にある場合と右側にある場合の2通り書かないといけないので、左側にある場合のみを示します。
// root を根とする部分木に対してスプレー操作を実行し、新たな根を返す。 // key を持つノードが部分木に存在する場合、それが新たな根となる。 // key が部分木に存在しない場合、最後にアクセスしたノードが根となる。 // 部分木は破壊的に変更される。 fn splay<K: Ord>(key: &K, root: Option<Box<BinaryNode<K>>>) -> Option<Box<BinaryNode<K>>> { if root.is_none() { return None; } let root = root.unwrap(); let new_root = match key.cmp(&root.key) { Ordering::Less => splay_left(key, root), Ordering::Greater => splay_right(key, root), Ordering::Equal => root, }; Some(new_root) } // key が root の左側にあるときのスプレー操作を行う。新たな根を返す。 fn splay_left<K: Ord>(key: &K, mut root: Box<BinaryNode<K>>) -> Box<BinaryNode<K>> { if root.left.is_none() { return root; } let mut left = root.left.unwrap(); if key < &left.key { // zig-zig // left-left の部分木の根に key を持ってくる left.left = splay(key, left.left); root.left = Some(left); // 右回転を2回行って left-left を根に持ってくる let new_root = rotate_right(root); if new_root.left.is_some() { rotate_right(new_root) } else { new_root } } else if key > &left.key { // zig-zag // left-right の部分木の根に key を持ってくる left.right = splay(key, left.right); // 左回転と右回転を行って left-right を根に持ってくる root.left = if left.right.is_some() { Some(rotate_left(left)) } else { Some(left) }; rotate_right(root) } else { // zig root.left = Some(left); rotate_right(root) } }
insert とか search とか
長くなってきたので、ここでは省略します。GitHub に全体のソースコードを上げているので、そっちを参照してください。
workspace/splay_tree.rs at master · nojima/workspace · GitHub
まとめ
NLL は最高。
テストクラスを継承するとインターフェイスのテストが捗る
User オブジェクトの永続化を行う UserRepository というインターフェイスがあるとします。
また、それを実装した2つのクラス InMemoryUserRepository と MySqlUserRepository があるとします。
これらのクラスのテストはどのように書けばよいでしょうか?
(テストフレームワークは JUnit5 です)
普通に考えると InMemoryUserRepository と MySqlUserRepository の2つのテストを個別に書かないといけないように思います。
しかし、これらのクラスはどちらも UserRepository として振る舞うはずなので、UserRepository のインターフェイスのみを使ってテストを書けば1回テストを書くだけで2つの具象クラス両方をテストできます。
例
UserRepository が以下のようなインターフェイスだったとします。
(パスワードをそのままデータベースに保存するのはアウトですが、例なので許してください)
interface UserRepository { // 指定した id を持つユーザーを取得する。 // 存在しないときは null を返す。 fun getUser(id: UserId): User? // 名前とパスワードを指定して新しくユーザーを作成する。 fun createUser(userName: UserName, password: Password): User }
実装として、InMemoryUserRepository と MySqlUserRepository があります。
class InMemoryUserRepository : UserRepository { private var nextUserId = 1L private val users = HashMap<UserId, User>() override fun getUser(id: UserId) = users[id] override fun createUser(userName: UserName, password: Password): User { val id = UserId(nextUserId) nextUserId += 1 val user = User(id, userName, password) users[id] = user return user } }
class MySqlUserRepository( private val dataSource: DataSource ) : UserRepository { override fun getUser(id: UserId): User? { // 略 } override fun createUser(userName: UserName, password: Password): User { // 略 } }
まずは、インターフェイスである UserRepository に対してテストを書きます。
テストクラスは abstract class にしておき、テスト対象である UserRepository は abstract val として宣言します。
internal abstract class UserRepositoryTest { abstract val sut: UserRepository @Test @DisplayName("getUser - 正常系") fun getUser() { // Setup sut.createUser(UserName("alice"), Password("open sesame")) // Exercise val user = sut.getUser(UserId(1)) // Verify val expected = User(UserId(1), UserName("alice"), Password("open sesame")) assertThat(user).isEqualTo(expected) } @Test @DisplayName("getUser - 存在しないユーザーを取得すると null が返る") fun getNonexistentUser() { // Exercise val user = sut.getUser(UserId(100)) // Verify assertThat(user).isNull() } @Test @DisplayName("createUser - 正常系") fun createUser() { // Exercise val user = sut.createUser(UserName("bob"), Password("secret")) // Verify val actual = sut.getUser(user.id) val expected = User(user.id, UserName("bob"), Password("secret")) assertThat(actual).isEqualTo(expected) } }
これでテストケースの定義が書けました。では、このクラスを継承してテストの実体を作ります。
まずは InMemoryUserRepositoryTest から。
internal class InMemoryUserRepositoryTest : UserRepositoryTest() { override val sut: UserRepository = InMemoryUserRepository() }
たった3行でした。
次は、MySqlUserRepositoryTest を書きます。
internal class MySqlUserRepositoryTest : UserRepositoryTest() { private val dataSource = /* テスト用 MySQL の DataSource を作成する処理 */ override val sut: UserRepository = MySqlUserRepository(dataSource) init { val flyway = Flyway.configure() .dataSource(dataSource) .load() flyway.clean() flyway.migrate() } }
MySQL を使う場合は DataSource を作ったり、テストケースごとにデータベースを初期化したりする必要があるので、InMemory よりもちょっとコードが増えています。 この例では Flyway を使ってデータベースの初期化を行っています。
この状態でテストを実行すると InMemory と MySQL それぞれに対して UserRepositoryTest で定義した3つのテストケースが実行されます。
2つの具象クラスに対するテストを共通化できたというわけです。
以上、テストクラスを継承することでインターフェイスのテストを行う例でした。
rust-protobuf で読み書きしてみる
rust-protobuf を使ってみる。
大まかな流れ
protoc をインストールする
Ubuntu ならこんな感じ:
sudo apt update sudo apt install protobuf-compiler
cargo build 時に proto をコンパイルするようにする
まず、コンパイルすべき proto ファイルを用意する。
以下のファイルを src/person.proto に置く:
syntax = "proto3"; message Person { uint64 id = 1; string name = 2; }
次に、Cargo.toml に以下を追加する:
[build-dependencies] protoc-rust = "2.0"
build.rs というファイルを Cargo.toml と同じディレクトリ に置く:
extern crate protoc_rust; use protoc_rust::Customize; use std::error::Error; fn main() -> Result<(), Box<Error>> { let proto_files = vec!["src/person.proto"]; protoc_rust::run(protoc_rust::Args { input: &proto_files[..], out_dir: "src/protos", includes: &[], customize: Customize { ..Default::default() }, })?; Ok(()) }
ここで out_dir に src/protos というディレクトリを指定したので、作成しておく。
mkdir src/protos
これで proto をコンパイルする準備が整った。あとは cargo build すればコンパイルされる。
cargo build # person.rs が生成されていることを確認 ls src/protos
コンパイルによって生成された struct を使って読み書きする
まず、Cargo.toml に以下の dependency を追加する:
[dependencies] protobuf = "~2.0"
次に生成されたモジュールを use できるようにする。src/protos/mod.rs を以下の内容で作成:
pub mod person;
次に main.rs に以下を追加:
mod protos; use protos::person::Person;
これで準備は整ったのでいよいよ読み書きしていく。
書き込み
以下のように、Person::new() で入れ物を作り、set_* で値を入れ、write_to_writer で書き出す。
use protobuf::Message; use std::fs::File; ... let mut person = Person::new(); person.set_id(42); person.set_name("Yusuke Nojima".to_string()); let mut file = File::create("/tmp/person.bin")?; person.write_to_writer(&mut file)?;
読み込み
デシリアライズしたいスライスを merge_from_bytes に渡すと読み込んでくれる。
use protobuf::Message; use std::fs::File; use std::io::Read; ... let mut file = File::open("/tmp/person.bin")?; let mut buffer = vec![]; file.read_to_end(&mut buffer)?; let mut person = Person::new(); person.merge_from_bytes(&buffer[..])?;
サンプルコード
サンプルコード全体は GitHub にアップロードしたので、断片じゃなくて動作するコードが読みたい人はこっちを参照してください:
workspace/rust-protobuf-sample at master · nojima/workspace · GitHub
参考にしたページ
rust-protobuf 自体にはあまりドキュメントがないけど、C++版と使い方がかなり似ているので、本家の C++ のドキュメントが参考になった。
Protocol Buffer Basics: C++ | Protocol Buffers | Google Developers
Transactional Database を作りたい
セキュリティキャンプ2018のデータベースの講義に関するツイートがTLに流れてきたのを見て、自分もデータベース作ってみたいなぁと思ったので作り始めることにした。 データベースを作るのは初めてなので、まずは「トランザクションのあるデータベース」と言い張れる最小限のものを作りたい。
ということで「ぼくのかんがえたさいじゃくのデータベース」の仕様を作った。明日から頑張る。
概要
- 表形式ではなく、key-value store にする
- key も value も String 型
- トランザクションをサポート
- トランザクション上で任意個のコマンドを実行できる
- ACID を満たす
- クライアントは逐次的に処理する
- データの総量がメモリに収まると仮定する
コマンド
以下の4つのコマンドをサポートする。
read KEY write KEY VALUE commit rollback
クライアントは TCP でデータベースサーバーに接続してコマンドを送りつける。
ACID
Atomicity
トランザクションの結果が、コマンドが全て実行された結果か、全く実行されなかった結果のどちらかになる性質。
Consistency
……このデータベースの場合、満たすべき制約は存在しない?
Isolation
トランザクションの過程が他のトランザクションから観測されない性質。 このデータベースではそもそも複数のトランザクションを同時に実行しないので自動的に満たされる。
Durability
成功したトランザクションの結果が(たとえデータベースやコンピュータがクラッシュしても)失われない性質。
設計
- Rust で作る。
- メモリ上に HashMap として key-value store を持つ。
- ディスクに WAL を書く。
- 起動時に WAL を先頭から全部読んで HashMap を再生する。
- このとき、WAL の末尾の未コミットのレコード列は truncate する。
- 中途半端に書かれた WAL のレコードは truncate する。このために WAL のレコードには CRC64 をつけておく。