[論文紹介] GConnect: A Connectivity Index for Massive Disk-Resident Graphs

授業で論文紹介したので，ここにメモ．

『GConnect: A Connectivity Index for Massive Disk-Resident Graphs』は，巨大なグラフに対してインデックスを作って，辺連結度クエリに高速に答える手法について議論した論文です．以下のような問題を考えます．

巨大なグラフGが与えられる．(例えば，頂点数10万，辺数100万とか)
G内の任意の2点s, tが与えられたとき，sとtの辺連結度を高速に計算せよ．

2頂点の辺連結度というのは，グラフから最小で何本辺を取り除けば，その2頂点を非連結にできるかで定義される量です． 

計算時間を気にしなければ，最大 s-t フローを求めるアルゴリズム(Dinic や Goldberg-Tarjan など)で連結度を計算することができます．しかし，これらのアルゴリズムは記憶領域へのランダムアクセスを要求するため，メモリに格納できないサイズのグラフに対しては非常に遅くなり得ます．情報検索への応用を考えると，(s, t)が与えられたときに，数秒で答えを返さなければなりません．そこで，厳密解を求めることを諦め，近似解を求めることにし，事前に巨大なグラフをメモリに収まるサイズまで圧縮しておくことを考えます．

グラフの圧縮は，辺サンプリングに基づいて行います．下図(論文中の図から引用)のように，グラフ内の各辺に対して，一定の確率 f でその辺をサンプルします．そして，サンプルされた辺による連結成分を縮約します．結果として，頂点数と辺数が小さくなったグラフができます．

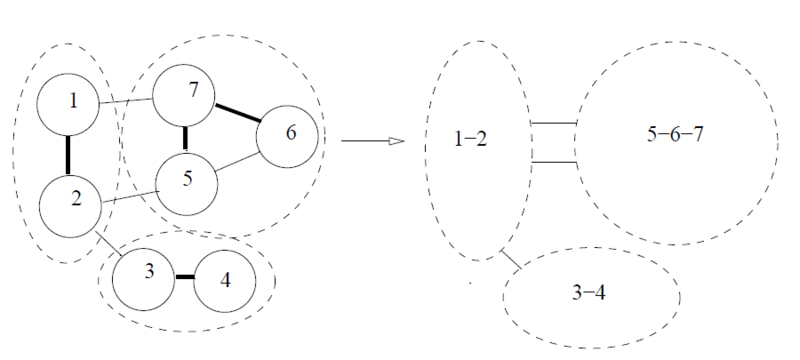
なぜこれで辺連結度の近似ができるのでしょうか？まず，辺連結度というのは，グラフの中の辺が比較的疎な部分で決まりやすいという性質を持っています．さらに，グラフの辺サンプリングは，辺が密な部分は，多くの辺がサンプルされ，一つの頂点に縮約されやすく，また，辺が疎な部分は，余り辺がサンプリングされず，縮約もされにくいという性質を持っています．よって，グラフの辺が疎な部分の構造が辺サンプリングによって保存されやすいため，辺連結度を概ね保存したまま，グラフを圧縮できるというわけです．

頂点対(s, t)に対応する，圧縮されたグラフの頂点対が(s', t')であったとします．ここで，s' ≠ t' とします．真のs-t辺連結度が C であるとすると，辺サンプリングによって正しくs-t辺連結度が求まる確率は少なくとも (1 - f)^C あります．(最小 s-t カットに含まれる辺がいずれも辺サンプリングによって選ばれない確率が (1 - f)^C です)

より高い確率で正しく辺連結度を求めるため，圧縮されたグラフを k 個作成し，それぞれの圧縮されたグラフで辺連結度を計算し，それらの最小値を答えとして返すことにします．(圧縮によって辺連結度が大きくなる場合は存在するが，逆の場合は存在しないので，最小値をとるのが良い)

圧縮されたグラフにおいて，s' = t' になってしまった場合は，辺連結度を計算できません．このような場合に対処するために，論文では，頂点サンプリングを使って圧縮したグラフを導入しています．詳しくは論文を読んでください．

現実のグラフを使った実験結果によると，圧縮によりグラフのサイズを 93% ～ 99% 程度減らすことができ，それによるエラーは6%以下にとどまっています．クエリの計算時間は，ナイーブな場合にくらべて 500倍程度速くなったようです．